Sebelum kita memahami materi himpunan, coba kalian sebutkan contoh-contoh dari hewan herbivora. Sebut saja ada sapi, kambing, kelinci, kuda dan yang lainnya. Kumpulan hewan-hewan tersebut bisa kita sebut sebagai himpunan hewan herbivora.
Bagaimana kalau himpunan nama-nama hari yang berawalan huruf B? Tidak ada kan. Lalu bagaimana cara menuliskan himpunan yang tidak memiliki anggota?
Semua pertanyaan-pertanyaan di atas akan kita ketahui jawabannya pada pembahasan himpunan berikut. Selain itu, kita juga akan memahami apa itu irisan, gabungan, selisih, dan komplemen dari himpunan. Yuk, simak ulasannya di bawah ini.
Pengertian Himpunan
Himpunan didefinisikan sebagai kumpulan dari objek tertentu yang memiliki definisi yang jelas dan dianggap sebagai satu kesatuan.
Coba perhatikan contoh berikut ini.
- Himpunan hewan berkaki dua
- Himpunan bilangan asli
- Himpunan lukisan yang bagus
- Himpunan orang yang pintar
Bisakah kalian membedakan yang merupakan himpunan dan yang bukan himpunan?
Yup contoh 1 dan 2 merupakan himpunan, sedangkan contoh 3 dan 4 bukan himpunan.
Buat yang masih bingung, begini alasannya….
Pada contoh 1 hewan berkaki dua, kita akan memiliki pendapat yang sama tentang hewan-hewan apa saja yang berkaki dua, misalnya ayam, bebek, dan burung. Semua setuju kan kalau hewan-hewan tersebut berkaki dua? Pasti setuju kan. Nah, hewan berkaki dua memiliki definisi yang jelas sehingga merupakan suatu himpunan. Untuk contoh 2 bilangan asli juga memiliki definisi yang jelas sehingga merupakan suatu himpunan.
Pada contoh 2 lukisan yang bagus dan contoh 4 orang yang pintar, keduanya tidak memiliki definisi yang jelas. Kata bagus dan pintar memiliki definisi yang berbeda untuk setiap orang, misalnya aku menganggap lukisan A bagus tapi kamu belum tentu mengganggap lukisan A bagus juga kan? Oleh karena itu, lukisan yang bagus dan orang yang pintar bukan suatu himpunan.
Nah, sekarang udah tau kan perbedaan himpunan dan bukan himpunan. Sekarang kita lanjut dengan mempelajari bagaimana cara menyatakan suatu himpunan.
Cara Menyatakan Himpunan
Secara umum, himpunan disimbolkan dengan huruf kapital dan jika anggota himpunan tersebut berupa huruf maka anggotanya dituliskan dengan huruf kecil. Terdapat beberapa cara penulisan himpunan, yaitu
yaitu dengan menyebutkan semua syarat ataupun sifat dari anggota himpunan tersebut di dalam kurung kurawal.
Contoh: A merupakan bilangan prima antara 10 dan 40
Ditulis menjadi A = {bilangan asli antara 10 dan 40}
- Dengan notasi pembentuk himpunan
yaitu dengan menyebutkan semua sifat dari anggota himpunan tersebut, dengan anggotanya dinyatakan dalam suatu variabel dan dituliskan di dalam kurung kurawal.
Contoh: A merupakan bilangan prima antara 10 dan 40
Ditulis menjadi A= {x |10 < x < 40, x ϵ bilangan prima}
- Dengan mendaftarkan anggota-anggotanya
yaitu dengan menuliskan semua anggota dari himpunan tersebut di dalam kurung kurawal dan tiap anggotanya dibatasi dengan tanda koma.
Contoh: A merupakan bilangan prima antara 10 dan 40
Ditulis menjadi A={11, 13, 17, 19, 23, 29, 31, 33, 37}
Himpunan Semesta
Himpunan Semesta didefinisikan sebagai himpunan yang memuat semua anggota ataupun objek himpunan yang dibicarakan. Himpunan semesta disimbolkan dengan S.
Sebagai contoh, misalkan A = { 3, 5, 7, 9} maka kita bisa menuliskan himpunan semesta yang mungkin adalah S = {bilangan ganjil} atau S = {bilangan asli} atau S = {Bilangan Cacah} atau S = {bilangan real}. Tetapi kita tidak menuliskannya sebagai S = {bilangan prima} karena ada angka 9 yang bukan termasuk bilangan prima.
Himpunan Kosong
Himpunan kosong didefinisikan sebagai himpunan yang tidak memiliki anggota. Himpunan kosong disimbolkan dengan Ø atau { }.
Sebagai contoh, misalkan B adalah himpunan bilangan ganjil yang habis dibagi dua. Karena tidak ada bilangan ganjil yang habis dibagi dua, maka A tidak memiliki anggota sehingga merupakan himpunan kosong. Ditulis menjadi B = { } atau B = Ø.
Himpunan Bagian
Himpunan A merupakan himpunan bagian B, jika setiap anggota A juga anggota B dan dinotasikan A ⊂ B atau B ⊃ A.
Contoh soal:
P = {1, 2, 3}
Q = {1, 2, 3, 4, 5}
Maka P ⊂ Q atau Q ⊃ P
Jika ada anggota A yang bukan anggota B, maka A bukan himpunan bagian dari B dan dinotasikan dengan A ⊄ B.
Contoh Soal:
Q = {1, 2, 3, 4, 5}
R = {4, 5, 6}
Maka R ⊄ Q
Operasi Himpunan
1. irisan
Irisan dari dua himpunan A dan B adalah himpunan yang anggota-anggotanya ada di himpunan A dan ada di himpunan B. Irisan antara dua buah himpunan dinotasikan oleh tanda ‘∩’
Contoh Soal:
A = {a, b, c, d, e}
B = {b, c, e, g, k}
Maka A ∩ B = {b, c}
2. Gabungan
Gabungan dari dua himpunan A dan B adalah himpunan yang anggota-anggotanya merupakan gabungan dari anggota himpunan A dan himpunan B. Gabungan antara dua buah himpunan dinotasikan oleh tanda ‘∪‘.
Contoh Soal:
A = {a, b, c, d, e}
B = {b, c, e, g, k}
Maka A ∪ B = {a, b, c, d, e, g, k}
3. Selisih
A selisih B adalah himpunan dari anggota A yang tidak memuat anggota B. Selisih antara dua buah himpunan dinotasikan oleh tanda ‘– ‘.
Contoh Soal:
A = {a, b, c, d, e}
B = {b, c, e, g, k}
Maka A – B = {a, d}
4. Komplemen
Komplemen dari suatu himpunan adalah unsur-unsur yang ada pada himpunan universal (semesta pembicaraan) kecuali anggota himpunan tersebut. Komplemen dari A dinotasikan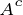 
(dibaca A komplemen).
Contoh Soal:
A = {1, 3, 5, 7, 9}
S = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
Maka 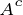= {2, 4, 6, 8, 10}
Gimana temen-temen materi tentang himpunan? Cukup mudah dipahami kan. Sekarang kamu jadi tahu apa itu himpunan, bagaimana cara menyatakanya, dan apa saja operasi pada himpunan. Selain itu, kamu juga tahu apa yang dimaksud dengan himpunan semesta, himpunan kosong, dan himpunan bagian.
Klik LINK untuk mengerjakan PR Bab Himpunan - 1
Klik LINK untuk mengerjakan QUIZ
