Pada kendaraan bermotor, baik mobil ataupun sepeda motor, dipasang sistem alat yang berfungsi untuk meredam kejutan. Sistem alat ini dinamakan shockabsorber, yang kebanyakan orang menyebutnya shockbreaker. Salah satu komponen shocksabsorber adalah pegas (pir spiral). Coba Anda bayangkan apabila kendaraan Anda tidak menggunakan shockabsorber. Pasti Anda akan cepat leiah dan tidak menyenangkan ketika berkendara. Pada saat berkendaraan meiewati jalan berlubang, berat kendaraan dan pengendara akan menekan pegas sehingga termampatkan. Pegas akan kembali ke bentuk semula pada jalan rata. Dengan demikian, pengendara hanya merasakan sedikit kejutan. Mengapa pegas tersebut dapat kembali ke bentuk semula? Apa manfaat pegas pada produk teknologi lainnya? Simak dan pelajari artikel ini dengan saksama.

Terdapat macam macam bentuk elastisitas, yaitu elastisitas zat padat, elastisitas pada pegas, dan energy potensial pegas. Dibawah ini adalah penjelasan dari masing masing bentuk dari elastisitas dan Contoh soal beserta cara penyelesaiannya.
Daftar Isi [hide]
Elastisitas Zat Padat
Elastisitas adalah sifat suatu benda untuk kembali ke bentuk awal segera setelah gaya yang mengenai benda tersebut dihilangkan. Benda yang dapat kembali ke bentuk semula setelah gaya yang mengenainya dihilangkan disebut benda elastis. Ketika Anda menarik pegas hingga bertambah panjang, pegas akan segera kembali ke ukuran semula setelah gaya tarik tersebut dihilangkan. Sebaliknya, benda yang tidak dapat kembali ke bentuk semula setelah gaya yang mengenainya dihilangkan disebut benda plastis. Contoh benda plastis antara lain plastisin, lumpur, dan tanah liat. Besaran-besaran yang berhubungan dengan sifat elastisitas benda antara lain sebagai berikut.
a. Tegangan (δ)
Tegangan adalah besamya gaya yang bekerja pada suatu benda pada luas penampang tertentu. Secara matematis, tegangan dirumuskan sebagai berikut.
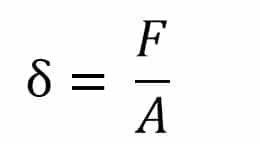
b. Regangan (e)
Regangan adalah perubahan relatif ukuran benda yang mengalami tegangan. Regangan dihitung dengan cara membanding- kan pertambahan panjang suatu benda terhadap panjang awalnya. Secara matematis, regangan dirumuskan sebagai berikut.
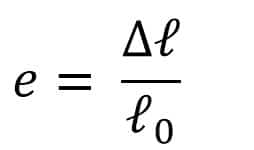
c. Modulus Elastisits (Modulus Young)
Modulus Young adalah besamya gaya yang bekerja pada luas penampang tertentu untuk meregangkan benda. Dengan kata lain, mddulus Young merupakan perbandingan antara tegangan dan regangan pada benda. Nilai modulus Young menunjukkan tingkat elastisitas suatu benda. Semakin besar nilai modulus Young, semakin besar pula tegangan yang diperlukan untuk meregangkan benda. Modulus Young dirumuskan sebagai berikut.
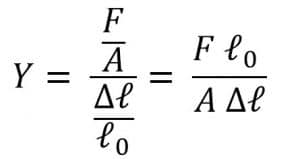
d. Batas Elastis
Sifat elastisitas benda memiliki batas sampai pada suatu besar gaya tertentu. Apabila gaya yang diberikan lebih kecil daripada batas elastisitas, benda akan kembali ke bentuk semula ketika gayp tersebut dihilangkan. Akan tetapi, apabila gaya yang diberikan lebih besar daripada batas elastisitas benda, benda tidak dapat kembali ke bentuk sem,ula. Benda secara permanen berubah bentuk.
Elastisitas pada Pegas
Pegas merupakan benda elastis karena dapat kembali ke bentuk semula ketika gaya pada pegas dihilangkan. Gaya yang dapat menggerakkan benda kembali ke bentuk semula disebut gaya pemulih.
a. Hukum Hooke
Pada tahun 1678, Robert Hooke menyatakan apabila pegas ditarik dengan suatu gaya tanpa melampaui batas elastisitasnya, pada pegas akan bekerja gaya pemulih yang sebanding dengan simpangan benda dari titik seimbangnya tetapi arahnya berlawanan dengan arah gerak benda. Pernyataan ini dikenal dengan hukum Hooke. Secara matematis, hukum Hooke dinyatakan sebagai berikut.
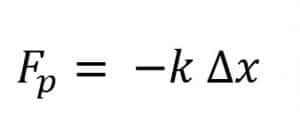
Tanda negatif pada hukum Hooke bermakna bahwa gaya pemulih pada pegas selalu berlawanan dengan arah simpangan pegas. Tetapan pegas (k) menyatakan ukuran kekakuan pegas. Pegas yang kaku memiliki nilai k yang besar, sedangkan pegas lunak memiliki k kecil.
b. Tetapan Gaya pada Benda Elastis
Dari pembahasan sebelumnya diketahui bahwa modulus Young dirumuskan sebagai berikut.
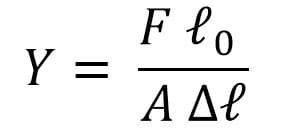
Dari persamaan di atas, besarnya gaya yang bekerja pada benda dapat ditulis sebagai berikut.
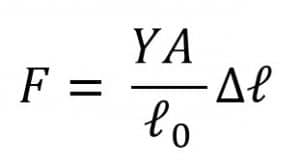
Berdasarkan hukum Hooke, besar gaya pemulih pada pegas sebesar F =-k ∆x atau F = -k ∆ℓ Dengan demikian, konstanta gaya pada benda elastis dapat dirumuskan sebagai berikut.
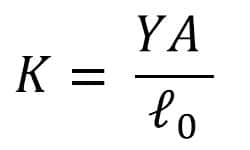
c. Hukum Hooke untuk Susunan Pegas
Sebuah pegas yang diberi gaya akan mengalami pertambahan panjang sesuai gaya yang diberikan padanya. Bagaimana jika pegas yang diberi gaya’berupa susunan pegas (lebih dari satu)? Berbagai macam susunan pegas antara lain sebagai berikut.
Susunan Seri pegas
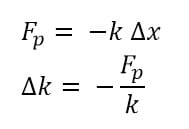
Pertambahan panjang pegas yang disusun seri merupakan jumlah pertambahan panjang kedua pegas. Jadi, tetapan pegas yang disusun seri dihitung:
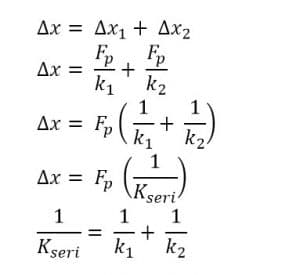
Jadi, ketetapan pegas yang disusun seri dihitung:
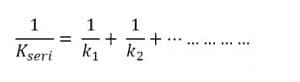
susunan parallel pegas
Gaya mg digunakan untuk menarik kedua pegas sehingga pertambahan panjang kedua pegas sama.

Energi Potensial Pegas
Energi potensial pegas merupakan kemampuan pegas untuk kembali ke bentuksemula. Berdasarkan hukum Hooke, besarnya gaya pemulih sebanding dengan simpangan benda. Hukum Hooke dapat dinyatakan dengan grafik seperti di samping.
Grafik F-∆x tersebut menunjukkan bahwa daerah yang diarsir merupakan usaha yang dilakukan untuk menarik pegas atau besarnya energi potensial pegas untuk kembali ke bentuk semula. Besarnya energi potensial pegas dihitung dengan langkah sebagai berikut.
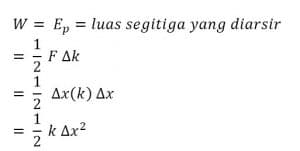
Contoh Soal !
1. Seutas kawat logam berdiameter 1,4 mm dan panjang 60 cm digantungi beban bermassa 100 gram. Kawat tersebut bertambah panjang 0,3 mm. Apabila percepatan gravitasi bumi sebesar 9,8 m/s2, hitunglah:
a. tegangan,
b. regangan, dan
c. modulus Young bahan.
Penyelesaian:
Diketahui
d = 1,4 mm
r = 0,7 mm = 7 x 10-4m
m = 100 g = 0,1 kg
g = 9,8 m/s2
ℓ0 = 60 cm = 0,6 m
∆ℓ = 0,3 mm = 3 x 10-4 mm
Ditanyakan :
a. δ
b. e
c. Y
Jawab:
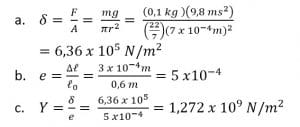
2. Sebuah pegas memiliki panjang 50 cm saat digantung vertikal. Pada saat diberi beban seberat 30 N, pegas bertambah panjang menjadi 55 cm. Berapakah konstanta pegas dan panjang pegas ketika ditarik gaya sebesar 45 N?
Penyelesaian:
Diketahui:
X0 = 50 cm = 0,5 m
X1 = 55 cm = 0,55 m
F1 = 30 N
F2 = 45 N
Ditanyakan :
a. K
b. X2
Jawab:

3. Seutas kawat sepanjang 1 meter ditarik dengan gaya 4 N. Luas penampang kawat tersebut 2 mm2 dan modulus elastisitasnya 1010 N/m2. Hitung pertambahan panjang kawat akibat gaya yang diberikan!
Penyelesaian:
Diketahui:
Y = 1010 N/m2
A = 2 mm2 = 2×10-6 m2
ℓ = 1 m
F = 4 N
Ditanyakan = ∆ℓ
Jawab:

4. Kawat A dan B terbuat dari bahan yang sama. Kawat A memiliki diameter tiga kali diameter kawat B dan memiliki panjang dua kali panjang B. Berapakah perbandingan antara tetapan gaya kawat A dan B?
Penyelesaian:
Diketahui :
Kawat terbuat dari bahan yang sama sehingga YA = YB = Y
DA = 3 DB
ℓA = 2 ℓB
Ditanyakan : KA : KB
Jawab:









 dan arah resultan vektornya adalah 22,3
dan arah resultan vektornya adalah 22,3 dan
dan . Nah,
. Nah, 


